archivierte Beiträge
MathePlus 4a/4b: Platonische Körper
- Kategorie: 06 Klassenarchiv Schuljahr 2009/2010
- Erstellt: Freitag, 11. Dezember 2009 21:42
- Geschrieben von Brigitte Reinhard
|
|
| MathePlus ist ein Förderangebot für Kinder, die mathematisch interessiert sind. In diesem Unterricht erhalten sie die Möglichkeit, in Kleingruppen besondere Themen zu erarbeiten, die selbstständige, logische, kombinatorische sowie kreative Denkleistungen und Problemlösungsstrategien erfordern. Die schwierigen Aufgabenstellungen sollen die Freude am mathematischen Denken wecken bzw. aufrechterhalten und somit Kinder mit mathematischen Begabungen angemessen fördern. |
| Mehrere Wochen lang beschäftigten sich die Mädchen und Jungen aus den Klassen 4a und 4b im Förderunterricht MathePlus begeistert mit dem Thema „Platonische Körper“. Über die Kenntnisse der geometrischen Körper des grundlegenden Mathematikunterrichts hinausgehend erhielten sie mit dieser Unterrichtseinheit ein anregendes und zugleich herausforderndes Lernangebot, um ihre mathematischen Begabungspotentiale weiter zu entfalten. |
| Neben mathematischen Begabungen wurden auch nichtkognitive Stärken wie Neugier, aufgabenorientierte Motivation, Kreativität, Selbstständigkeit, Fleiß, Ausdauer, positive Einstellung gegenüber sich stellenden Herausforderungen, hohe Frustrationstoleranz, gutes Selbstkonzept verbunden mit realistischer Selbsteinschätzung, Konzentration, Merkfähigkeit, Anpassungsfähigkeit an einen Partner/eine Gruppe, Spaß an Kommunikation, präzise Ausdrucksweise u. a. gefördert. | |
| Die Aufgabenstellungen waren so offen gewählt, dass sie dem Erkundungsdrang der Kinder entgegenkamen und ausreichend Raum boten, eigene Problemlösungsstrategien und das Erkennen von Gesetzmäßigkeiten und Regelhaftigkeiten zu entwickeln, zu erörtern und sich über Denkprozesse auszutauschen. | |
| Die Aufgabenstellungen | |
| 1. Baue platonische Körper. Für platonische Körper gelten folgende Bedingungen: | |
|
|
|
2. Finde die Namen der platonischen Körper mit Hilfe dieser Links im Internet heraus. 3. Ist ein Doppeltetraeder ein platonischer Körper? Begründe deine Meinung. 4. Untersuche die platonischen Körper hinsichtlich der Form der Flächen und der Anzahl der Flächen in jeder Ecke. Trage die Ergebnisse in einer Tabelle ein. 5. Untersuche die platonischen Körper hinsichtlich der Anzahl der Flächen, der Anzahl der Ecken, der Anzahl der Kanten. Trage die Ergebnisse in die Tabelle ein. 6. Die Eulersche Polyederformel: Überlege dir mit Hilfe der Tabelle einen Zusammenhang/eine Regel zwischen der Anzahl der Flächen, Ecken und Kanten. Finde eine einfache Gleichung, in der nur eine Addition und eine Subtraktion vorkommen. 7. Abwicklung eines Tetraeders: Rolle das Tetraeder mit jeder Fläche einmal auf einem Blatt Papier ab und zeichne die Kanten nach. Was entsteht aus deiner Zeichnung? 8. Stelle Papiermodelle aller platonischen Körper aus den Polyedernetzen her. Welcher Körper gehört zu welchem Netz? |
|
| Entdeckendes und handelndes Lernen | |
 |
 |
 |
 |
|
|
|
 |
 |
| Präsentation der Arbeitsergebnisse: Die 5 platonischen Körper | |
|
das Tetraeder: 4 gleichseitige Dreiecke |
das Hexaeder: 6 Quadrate |
 |
 |
|
das Oktaeder: 8 gleichseitige Dreiecke |
das Dodekaeder: 12 regelmäßige Fünfecke |
 |
 |
|
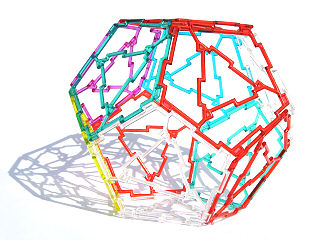das Ikosaeder: 20 gleichseitige Dreiecke |
|
 |
Das Ikosaeder bereitete allen Kindern gehöriges Kopfzerbrechen. Doch zum Schluss rief die erste Gruppe: "Ich hab's!" Oder wie Platon auf griechisch gesagt hätte: "Heureka!" Rein zufällig bastelten die Kinder der Wer zum Schluss immer noch Lust auf platonische Körper hatte, konnte sich einen DODEKALENDER - einen Kalender für 2010 in Form eines Dodekaeders - basteln. Und alle Mädchen und Jungen von MathePlus hatten Lust! |
| Die Faszination der platonischen Körper (regelmäßige/reguläre Polyeder) | |
|
|
|
| Unter den Polyedern (Vielflächnern) sind besonders die fünf regelmäßigen Polyeder die „ordentlichsten“ und faszinierendsten: keine Ecke und keine Fläche ist herausgehoben. Regelmäßigkeit hatte für die Gelehrten der Antike etwas Göttliches. Benannt wurden sie nach dem griechischen Philosophen Platon, der wie viele andere griechische Philosophen vor ihm nach den Grundbausteinen der Welt suchte - den fünf Elementen. Das Tetraeder wurde dem Feuer zugeordnet, das Oktaeder der Luft, das Hexaeder der Erde, das Ikosaeder dem Wasser und das Dodekaeder dem Himmel. Der Name der platonischen Körper besteht aus der griechischen Vorsilbe für die Seitenzahl und der Endsilbe -eder: tetra = 4, hexa = 6, okta = 8, dodeka = 12, ikosa = 20. | |
| Die auffällige Regelmäßigkeit der platonischen Körper ist auch außerhalb der Mathematik für den Menschen interessant: Spielewürfel sind heutzutage nicht nur klassisch sechsflächig (Würfel), sondern haben ebenso Formen anderer platonischer Körper. In der Natur besitzen einige Kristalle annähernd ähnliche Formen wie die platonischen Körper und begeisten die Menschen mit ihrer Schönheit. Auch in der Bildenden Kunst verarbeiteten moderne Künstler wie Escher und Dali platonische Körper als Motive in ihren Werken. | |
Klasse 4a zur gleichen Zeit ihre Martinslaterne, die die Form eines Ikosaeders hatte. Aber das erkannten sie erst etwas später. Tja, Mathematik ist eben überall!