| Die Kinder der Klasse 3a und 3b probierten es im MathePlus-Förderunterricht aus. In diesem Förderunterricht beschäftigen sich die Jungen und Mädchen mit mathematischen Problemen, die in der Regel nicht in den Mathematik Lehrwerken zu finden sind und die kreative, logische, kombinatorische und experimentelle Lösungen erfordern. |
| Vor Beginn des Färbeexperimentes wurden die Mädchen und Jungen nach ihrer Vermutung zum Vierfarbenproblem befragt. Viele konnten es sich nicht vorstellen, dass vier Farben zum Färben z. B. einer Karte von Afrika ausreichen sollen, wobei die aneinander grenzenden Staaten nicht dieselbe Farbe haben dürfen. Nein, dafür hat Afrika einfach zu viele Länder! |
| Nun wurde das Vierfarbenproblem experimentell überprüft, was gar nicht so einfach war. Nicht immer klappte der erste Versuch auf Anhieb. |
 |
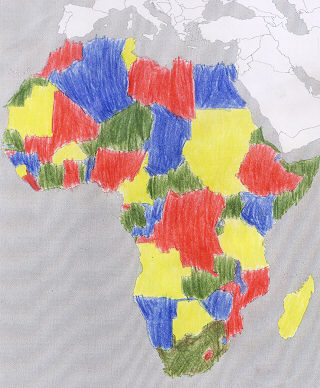 |
| 1. Färbebeweis von Anna J., 3b |
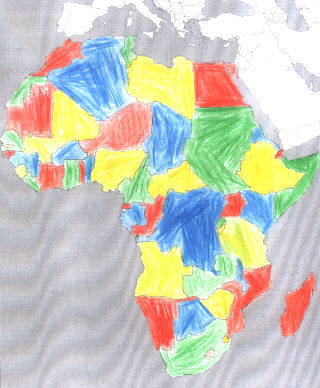
2. Färbebeweis von Fabian M., 3a |
|
|
 |
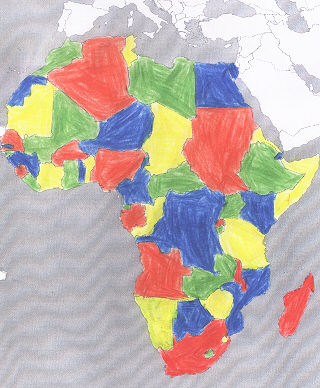 |
| 3. Färbebeweis von Justin Sch., 3b |
4. Färbebeweis von Niklas E., 3a |
|
|
| Um diesen Beitrag besonders für die jüngeren Leser unserer Homepage spannender zu machen, haben wir eine Landkarte mit Fehlern dazwischengemogelt. Hast du sie entdeckt? |
| Lösung: Karte 3 |
| Die Lösung wird sichtbar, wenn du mit der linken Maustaste die scheinbar leere Stelle hinter dem Wort "Lösung" markierst. |
|
|
| Die Vermutung von Francis Guthrie wurde durch diese Färbeversuche von den Kindern des MathePlus-Kurses experimentell bestätigt. Vier Farben reichen tatsächlich zum Färben einer Karte aus! Aber Mathematiker wollen eine Behauptung immer erst rechnerisch beweisen, bevor sie anerkennen, dass sie stimmt. Ihnen genügt es nicht, sie einfach nur durch einen Versuch auszuprobieren. Erst vor ungefähr 20 Jahren gelang dies zwei amerikanischen Mathematikern endlich mit Hilfe eines Computers. Dieser Beweis wurde deshalb so berühmt, weil zum ersten Mal ein Computer zur mathematischen Beweisführung eingesetzt wurde. |






